Volume Scale Factor
This chapter explores volume scale factor. It explores the connection between linear scale factor and volume scale factor for similar shapes and calculating lengths and volumes of similar shapes.
Cuboid Volume Scale Factor
Below is a cubiod whose volume is 60cm². Suppose we wanted to enlarge the cubiod by a linear scale factor of 2. We know that the volume will be different between the enlarged shape and the original shape.
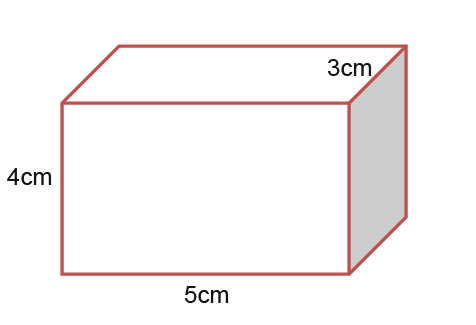
We want the new shape to be enlarged by a scale factor of 2 from the original shape. That must mean that the new cuboid will be twice as deep as the original cubiod, twice as long and twice as high.
| Old Volume | 3 x 4 x 5 = 60cm3 |
|---|---|
| Linear Scale Factor | x2 x2 x2 x8 |
| New Volume | 6 x 8 x 10 = 480cm3 |
Here can form a rule which says that if the lengths are 2 times bigger then the volume is 23 times bigger. Thus;
![]()
Example 2
The following vases below are similar. The bigger vase has 45cm length high while the smaller one is 15cm high. The small vase has a volume of 0.7 litres. Suppose we wanted to find the volume of the bigger vase.

First we have to find the linear scale factor. To find the linear scale factor we divide the biggest with the smallest volume. That is;
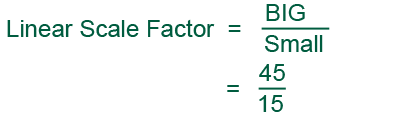
We know the linear scale factor is a 3. Now we need to find the volume scale factor.
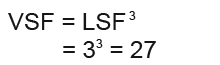
Since we know the volume scale factor we’re able to find the volume.
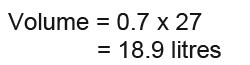
Example 3
The next example will involve applications of volume scale factor. Suppose a butter package manufacturer wanted to design a box which will increase the size of the package such that it holds 10% more butter, the current package if 10cm.
First we find the volume scale. The volume scale factor is 1.1 after adding 10%. We know that the linear scale factor is;
![]()
That is;
![]()
So the length of the larger package is;
![]()
