Area and Volume scale factor
Summary
Two figures/shapes may be identical in shape but generally not in size. The following shapes will always be similar in shape but not in size.


Linear scale factor
A shape can be transformed into another similar shape by adjusting its size through enlargement/reduction by using a scale factor. In this process all dimensions of the shape must stay proportional to each other (i.e the lengths, heights, or widths)
For example a scale factor of 2 means that the new shape is twice the size of the original shape. A scale factor of 3 means that the new shape is three times the size of the original.
To carry out enlargements/reductions you must first find the scale factor. To find the enlargement scale factor you divide the dimensions of the big shape by the small shape.
![]()
To find the shape reduction scale factor you divide the small dimensions by the big dimensions.

Below is an example.
Example: The following shapes abcd and ABCD are similar. Find the length of CD.
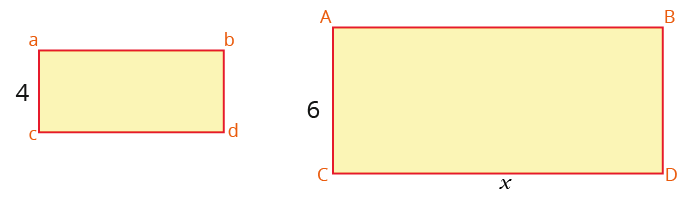
Answer: Here we have to find the length of the bigger rectangle. We shall therefore be calculating an enlargement scale factor first.
![]()
Notice we have used the corresponding lengths. The rectangle ABCD is 1.5 times bigger than rectangle abcd. We therefore multiply the width of the smaller rectangle with the enlargement scale factor to find the size of the bigger width.
![]()
Area Scale Factor
Area scale factor can apply to any shape provided you have at least one of the corresponding quantities (areas or lengths) For example here are two triangles;
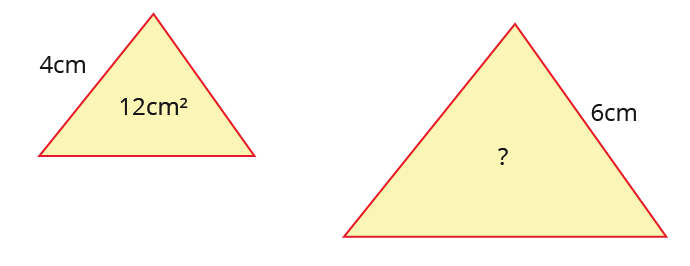
There are simple steps you will take to find the area of the large triangle;
In general to find the scale factor we divide the large quantity with the small quantity.

![]()
![]()
The area for the large shape is 27cm2
Volume Scale Factor
The same strategy applies to volume scale factors, except you have to be aware that volumes are cubic roots. For example your might have the following two bottles whose lengths are known and just one volume, and you have to find the other volume.

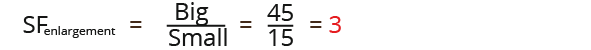
![]()
![]()

thx so much for this! helped a ton, and now i can finally do this!!!
Hello Shanea,
I am very glad to that this page helped you a lot.
how do you work out the length of the smaller or bigger one?
e.g the shapes are similar. the volumes are given and 1 length.
work out other length, x, in cm to 1 d.p
PLEASE HELP
Wow this was so helpful! It really helped bring my grades up lol xD
what do you do to find the smaller volume
OMG TNX SO MUCH
IT HELP ME SO MUCH
TNXTNXTNX
xoxoxoxo
Thanks for the info,
however, you should also include the relationships that the scale, volume and area scale factors have with each other. Otherwise this was quite helpful.