Completing the square

In this chapter we’re going to explore completing the square. You will understand how to the square, and also be able to use complete the square to solve quadratic equations.

Example

The following is a quadratic expression x² + 8x.
We want to write it as a square (x+4)².
Let us try to expand (x+4)², which we get;

Now let us remove the brackets and see what we get.

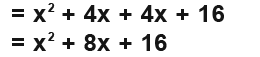
Note that the above expression includes the expression in question.
What would we have to do to (x+4)² to make it equal to x² + 8x? Because now we know that;

We would have to subtract 16 and whenever we subtract, add, divide or multiply in one side we must do to the other side as well. So;

When we go from x² + 8x to (x+4)² this is called making the sqaure. When we take away 16 this is called completing the sqaure

Example 2

Here is another even harder example.
Complete the square for the following expression; x² – 14x -5
First let’s deal with one part of the expression. This part is shown in brackets.

Now let’s make the square from (x² – 14x). This becomes;

Remember we still have -5 at the end, so expression becomes;

…which becomes;

It is as simple as that.

Solving quadratic equations

Now let’s use completing the square to solve quadratic equations. The following is a quadratic equation to solve;
x² – 12x -5 = 0
First we complete the square;

…which becomes;

Here we solve the equation as usual. Take 41 to the other side.

Now we square root both sides.

And simplify…


The x value is either;

…or

We have managed to solve the equation using completing the square.