Logarithms
The logarithm of a number to a given base is the exponent to which the base must be raised in order to produce that number. In simple description the logarithm is the power of a number (called the base) to give a number. The following example might make better sense. The logarithm of 100 to base 10 is 2. Notice the logarithm is the power that is called the logarithm of the produced number for a given base 10.
Mathematically we try to make the power x of a number the subject provided we have the answer. The above can be written as;
In general we say that:
Logarithms are particularly useful with functions, I know you might ask in which case would I want to know the power of a number in a mathematic expression but there might come a time when you might.
Work out example
Work out log5 125
We’re simply trying to find the value of x for this expression 5x = 125. So what power of base 5 gives 125? The answer is simply a 3. So;
log5 125 = 3
Rules of Logarithms
Like indices logs have certain properties too and the concepts are similar.
Logarithms rule 1
Working out loga a. we need the value of x so that ax = a. In this case x = 1 so; loga a = 1 This is the first rule of logarithms, it simple and straight forward. Any number to the power of 1 is equal to that number. When a number/base has a power of 1 the answer is that number/base, or you could think when a base has a value of x and the answer is the base x is equal to 1 (the logarithm)
Suppose you had to workout loga 1 We need a value of x so that ax = 1. In indices any number to the power of 0 is a 1, so in this case the x value would have to be a 0 so that the answer is a 1. This justifies the second; loga 1 = 0
This rule is a perfect example of the indices rule where any number to the power of -1 is equal to 1 divided by that very number, for example 5-1 = 1/5 If we had to work out the above rule loga (1/a) we would need to find the value x so that ax = (1/a) and that value would be a -1 This justifies the above rule.
Adding two logarithm equation we can use the indices rule of multiplying two powered numbers. We could simplify loga m + loga n as we did with the above rules to transform it into the rule above. Let’s break down the equation into two parts. In the first part we’re trying to find the value of;
x = loga m or ax = m
In the second part we’re trying to work out;
y = loga n or ay = n
In the indices rules we know that
ax x ay = ax+y
Try to think about it and realise that;
ax+y = mxn
This would mean that; loga mn = x+y = loga m + loga n
This justifies the above logarithms rule that; loga m + loga n = loga mn
You can relate the subtracting of two logarithms with the indices rule of dividing two powered numbers in reverse of course. If we break down the logarithms equation: loga m – loga n In the first part we’re trying to find the value of;
x = loga m or ax = m
In the second part we’re trying to work out;
y = loga n or ay = n
In indices rules we know that;
ax/ay = ax-y
So;
ax-y = m/n
This means that;
loga (m/n) = x – y = loga m – loga n
This justifies the above logarithms rule that; loga m – loga n = loga (m/n)
For this rule you have to understand the addition logarithm rule. Suppose you have to find out loga mn Notice here that we have the number whose logarithm is n with a base a You might find it hard to grasp the logicalness this particular rule out of all the others but all you have to do is remember it. To find the above logarithms would be the same as finding;
loga m x m x m … x m multiplying m by m n times. This is the same as the additional logarithms described above. This will also transform to;
nloga m
This justifies all equations in the form;
loga mn = nloga m
To simplify the following equation which is part of the rule about loga (1/y)
loga (1/y) is the same as loga 1 – logay
But we know that; loga 1 = 0 from one of the logarithms rules already described, which means;
loga (1/y) = 0 – loga y
which is equal to: – loga y
This completes the rules for logarithms and below are all the rules you will need to learn for logarithms;
Logarithms without base
Some times we write logs without the base. Logs without base usually means they have a base of 10, this is also similar to the log button on the calculator. It has base of 10. For example you might have;
In such case you assume that the base is 10.
________________________________________________________________________________________________________________________________
Logarithms
Introduction
Logarithms was invented to aid mathematicians who handled long and complex calculations. Although invented by Joost Burgi, it was publicised by John Napier in 1614, in a book titled Mirifici Logarithmorum Canonis Descriptio (Description of the Wonderful Rule of Logarithms). Logarithms has a way of reducing complex calculations into simple ones. In this article, we will be looking at how we can use logarithms and also discuss the various rules of logarithms.
Definition
In terms of a definition, we can say that the logarithm of a number say b to the base of a number say a, is the exponent to which a must be raised to give b. Let’s simplify that definition:
We know that
a x a x a x a=a^4
Based on this,
log_a〖a^4=4〗
In numerical terms,
3 x 3=3^2
Therefore,
log_3〖3^2=2〗
And another example for you to try your hands on
What is
log10000?
At this point, it is pertinent to mention that when the base is not included, then it is assumed to be base 10. So the above question could also have been written as
log_1010000
Easy isn’t it?
The answer to that is…….. you got it….4! This is because
log_10〖10000= log_10〖〖10〗^4=4〗 〗
Good. Before we move on to the rules in logarithms, one more important thing to note. The examples above used numbers which are easy to find an exponent for. What if we are told to find the log of say 5 to base 3?
log_3〖5= ?〗
This entails that we find an exponent such that 3 to the power of that exponent yields 5. Thankfully, the originators of logarithms also provided what we call log tables. You may not have heard of this because today instead of log tables, we simply use our calculators. However back in the days before the advent of calculators, mathematicians used log tables. These tables documented various possible exponents for logarithms with bases ranging from 2 to 10. Thankfully, you don’t need to use the table today. However, our modern day scientific calculators give logarithms in base 10. Since the above is in base 3, we will need to perform some manipulations before arriving at an answer. This brings us to the rules of logarithms.
Rules of logarithms
The first rule involves the change of base. It simply states that
log_ab= log_cb/log_ca
The change of base rule allows us to easily change the base of a logarithm to another. Let’s try this with the previous example. It is already in base 3 so let’s try and change it to base 10 which will then enable us use a calculator to solve.
log_35= log_105/log_103
The above can now be easily simplified using a calculator. Depending on what type of calculator you are using, simply press ‘log’ and then ‘5’ to find log5 on your calculator. Do same for log3. If you have done the right thing, then your answer should be
log_105/log_103 = 0.6990/0.4771=1.4651
Let’s try one more example. Find log_210.
First step is to change the base
log_210= log_1010/log_102
The numerator is easy to evaluate without the need for a calculator. It’s simply 1 because log101 = 1 like we discussed earlier but you can use a calculator to confirm.
For the denominator, as usual, just press ‘log’ and ‘2’ on your calculator and you should get the answer below.
log_210= log_1010/log_102 = 1/0.3010=3.3223
Rule 2
We will now look at four other rules – quotient, product, power and root.
Quotient and Product
The quotient and product rules are related and as such, we will discuss them together. Say we have to find the following:
log_10〖3/4〗
The quotient rule states that
log_10〖3/4= log_10〖3- log_104=0.4771-0.6021= – 0.125〗 〗
On the other hand, as you may already have guessed, for product rule,
log_10〖3 x 4= log_103+ log_104=0.4771+0.6021=1.0792〗
In most cases, examples may not be as straightforward as above. For example, try and figure out how to solve the examples below:
Find log_327
Find 64
Once you have tried it, you can check out the solution below.
In this case, since the base in is 3, we can either solve by changing bases or we can simplify further by reducing 27 to 3 x 9 or 3 x 32
log_327= log_3〖3 x 9〗= log_3〖3 x 3^2= log_3〖3^1+ log_3〖3^2= 1+2=3〗 〗 〗
Simple isn’t it? Let’s try (ii)
In this case, we can simplify 16 to log_264=log_2〖256/4〗=log_2〖2^8/2^2 = log_2〖2^8- log_2〖2^2 〗=8-2=6〗 〗
There may be easier ways of solving the examples above. They were simply used to demonstrate the product and quotient rules.
Now let’s take a look at the power rule. It simply states that
log_a〖x^y=y log_ax 〗
Using a numerical example, say we have to find log_264
We can simplify this further to
log_2〖2^6 〗
Using the product rule, we then have
log_2〖64= log_2〖2^6=6 log_22 〗 〗
But we know that log_22=1 (scroll up if you need to understand how we got this). Therefore,
log_2〖64= log_2〖2^6=6 log_2〖2=6*1=6〗 〗 〗
That explains the power rule.
Finally, the root rule
The root rule is a derivative of the power rule and I will explain why using the example below
log_a√(b&x)
The above can be re-written as
log_a〖√(b&x )= log_a〖x^(1/b) 〗 〗
And if we remember from power rule, we can re-write this as
log_a〖√(b&x )= log_a〖x^(1/b)=(1/b) log_ax 〗 〗
Or
(1/b) log_ax= 〖(log〗_ax)/b
From the above, we can thus simplify the root rule as
log_a√(b&x)= (1/b) log_ax= 〖(log〗_ax)/b
As usual, let’s try this with an example
log_10〖√100= log_10〖〖100〗^(1/2) 〗=(1/2) log_10〖100=(1/2)*2=1〗 〗
So that explains logarithms and its rules!
However before we round up, just one interesting thing to note. What if you are told to find
log_51
The interesting this about number ‘1’ in logarithm is that because we know that ‘anything’ raised to the power of 1 is zero, then the answer to the above is zero.
log_5〖1= 〗 log_5〖5^0=0〗
That base which is 5 in this case can be any base and as such, this applies to any base of the logarithm.

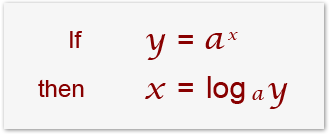


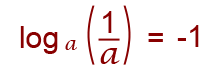


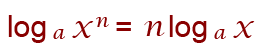
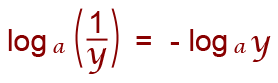


It is realy great and it helping us alot..but u mst add more examples on a given rule.e.g log rules
Hello Gilbert,
I will be adding more examples soon.
The discovery of logarithms by Napier in 1614 is certainly the first major British contribution to mathematics and could well be the most important maths discovery of all time. Most modern mathematicians have no idea how Napier did it , but we can say that the underlying sine tables played a crucial part. Directly related to logarithms was the discovery by Nicholas Mercator of the area under a symmetrical hyperbola measuring the logarithm of the distance along the x axis. The integration of the hyperbola equation produced a very useful equation for logarithms, which Isaac Newton succeeded in reversing in 1676 to produce the infinite series for antilogarithms or e, which otherwise we would not know about.
Napier’s discovery of logarithms in 1614 was based on a table of sines with 0.9999999 just below sine 90 degrees as the base which is raised to successive powers. Initially the results are nearly equal to he shortfall from 1.0000000. It would be a very onerous task to raise these powers from sine 90 degrees to sine 1 degree, but this would be helped by sine 75 degrees equalling 0.9659258 being raised to the power of 10 and equalling sine 45 degrees equalling 0.7071068, the log of which is 3465736.
Further to my comment of 21 January 2014, the little known fact that sine 75 degrees raised to the power of 10 equals sine 45 degrees can be computed as follows. Sine 75 degrees can be expressed as sine (45 + 30) which can be expanded into
(3^[0.5] +1)/(2 X2^[0.5]) which raised to the power of 10 equals sine 45 degrees.
Napier and Regiomontanus before him knew the formulae for constructing sine and cosine tables. Basically this is sin (2u) = 2sinu. cosu. This can be converted into sin(2u) = 2sinu. (1 -[sinu]^2)^(0.5), so that if the sine of a particular angle is known then the cosine of that angle can be calculated, also the sine of half that angle can be calculated by quadratic equation. The correct sine of 75 degrees can therefore be calculated from bisecting sin 30 degrees ( which is 1/2) to give the sine of 15 degrees which is the cosine of 75 degrees, from which the sine of 75 degrees can be computed.