Quotient Rule
The quotient rule can be used to differentiate fractions or find derivative of a fraction function, In this topic I will be showing you how to find the derivative using the quotient rule. the following is the quotient rule.

If the function is a function such as;
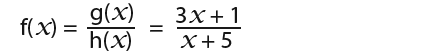
Trying to derive the above function would take a very long time and would be harder to derive. Let us try to derive it. We could rewrite the function as the following;
![]()
We could then use the product rule. The product rule in calculus is used to find the derivatives of products of two or more functions. The product rule is defined as;
![]()
…or we could write it in the Leibniz notation as;
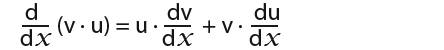
We’re trying the find the derivative of the above function using the product rule, we get;
![]()
I won’t go so much in the product rule since this section is about the Quotient rule. This is to show you how complex it would be without using the quotient rule. You can read more about the product rule here <= We can simplify further to get;
![]()
We can take out the factor to get;
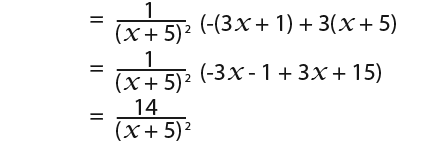
This is such a very long process. However if we used the quotient rule below;

…we get…
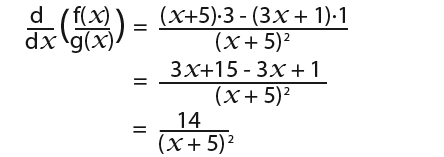
This is much simpler and quick. Below we shall look at how to derive various functions using the quotient rule.
Deriving the Quotient rule
Suppose we have a function in the form;

We’re trying to find f’(x) this is also the same as;
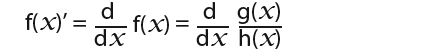
If f(x) is;

…that must mean that;
![]()
The product rule can be used here (since g(x) is a product of two functions), we can show that;
![]()
…for the equation above we need to make the derivative of f’(x) the subject, so we get;
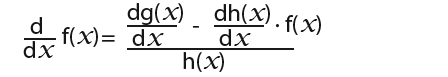
We know that;

…so we get;
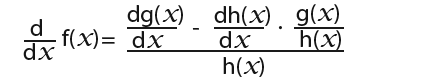
…this simplifies to;
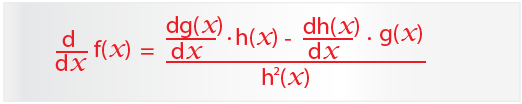
The following shows how to find derivatives of various functions using the quotient rule. Read through this section if you want to look at more examples and build your confidence.
Worked out example
Differentiate the following function using the quotient rule; 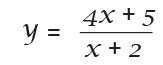
To differentiate the above function, we shall need to find the values for the letters in the quotient rule, then replace the letters with the values to find the differentiation.
The above is the differentiation for the function in question.
Example 2
Differentiate the following function.
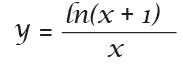
I have used the chain rule to differentiate In(x+1). So now I can go ahead and use the quotient rule.


We need to get rid of the fraction at the top so we multiply through the top and bottom.
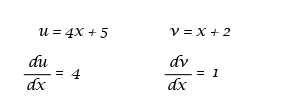
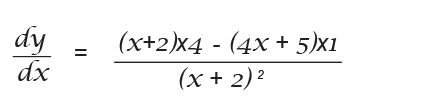
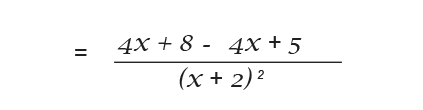
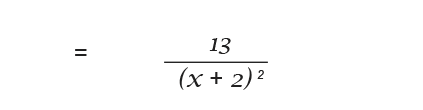
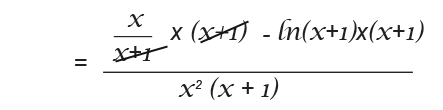
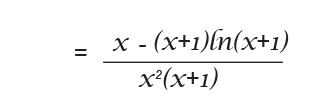

you got the quotient rule fucking wrong
It should be a minus sign on the top of the Quotient Rule equation
The quotient rule here is incorrect and is one of the first that comes up when you Google quotient rule images, it would be helpful if it was removed or corrected so people don’t find themselves going down blind alleys.
Sorry about that T.
That must have been an error while creating the images. I have corrected it now. It should be a minus. I hope Google will pick up the image sooner.
I will be updating this entry very soon to make it more clear with more examples.