Solving differential equations by using integration
In this article we shall look at how to solve differential equations by using integration. Here you’ll learn how to solve simple first order differential equations by the process called separation of variables. The following rule is known as separating the variable
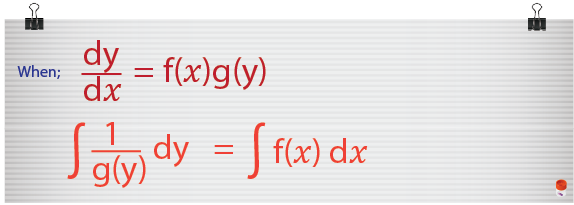
Example
In this example we shall find the general solution to the differential equation;
![]()
We know that the rule for the separation of variables states that;
![]()
So we will need to rewrite the expression into the form;
![]()
…that is;

Now we shall separate the variables to get;
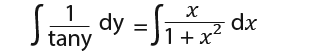
We know that coty = 1/tany;
![]()
We integrate to get;
![]()
Here we can rewrite c to ln|k| so we get;
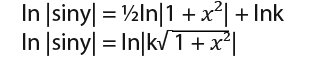
We can get rid of ln to get;
![]()
Example
Here is another example; Find the particular solution of the differential equation;
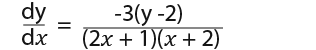
…given that x=1 when y=4.
We first need to separate the variables;
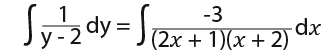
For the RHS we will use the partial fractions, i.e;
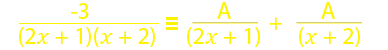
We rewrite the integral using partial fractions;

Now we can integrate. This time we shall use +ln k instead of +c.
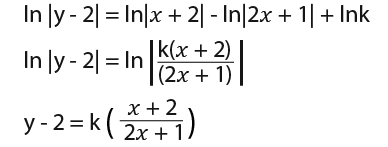
Now we shall use the condition that x=1 when y=4 by substituting the values in the general solution we have found in turn to find the value of k.
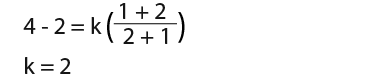
Now we shall substitute k=2 into the expression above and rewrite it in the form y=f(x);
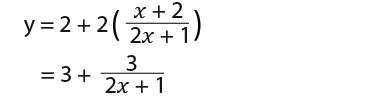

make things more interesting
Hi,
Thanks for the suggestion. Is the article too boring?