Trapezium rule
The trapezium rule takes advantage of the are of a trapezium formula:
The rule works by splitting the area under a curve into a number of trapeziums we could find the area for. For example consider the graph in the following diagram,
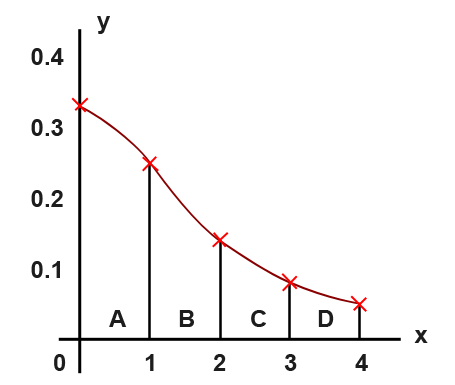
The area below the graph curve has been split into a number of trapeziums. These trapeziums have been noted by letters A, B, C, and D
Trapezium rule Examples
Find the area between the x-axis and the curve y = x2 + 2 between x = 1 and x = 5 using the trapezium rule with 4 strips./
Example
Answer
Explanation
First let’s draw a table to find out the y values.
| x | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| y | 3 | 6 | 11 | 18 | 27 |
So now we can use the trapezium rule. The trapezium rule states that as above:
The h is the height of the trapeziums or very simply the intervals between the x values. In the above table we have x values ranging from: 1, 2, 3, 4, and 5 The distance between these values is 1
The answer for the area between the curve of y = x2 + 2 is 50 square units

wow, this is great and easie
Thanks, I am glad you found it easy. I have just added a few missing details that I forgot to add. I hope you understood everything.
this ti the first time i come across Trapezium unfortunately i still do not understand the process
Thank u.. Finally I got the trapezium rule.. The explanation was straight to the point..