Trigonometry Missing Angles
Measuring angles
Trigonometry helps us to calculate angles in shapes. Consider the following triangle.
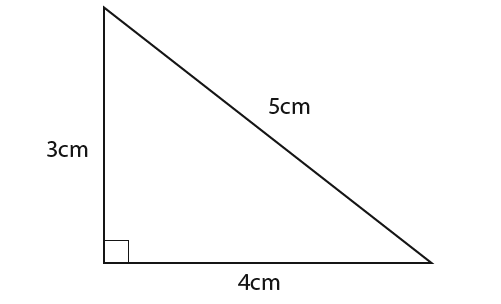
You could take a protractor and measure the unknown angles in the triangle. We can label the sides of the triangle
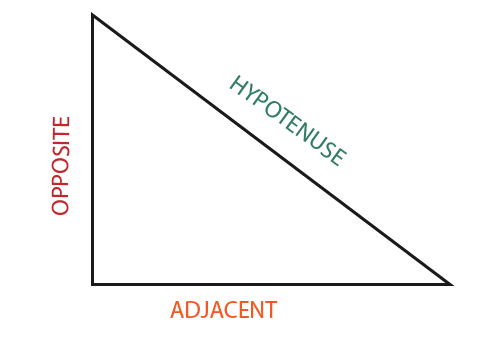
- Hypotenuse: The Hypotenuse is always defined as the longest side of a right angled triangle.
- Opposite: The ‘Opposite’ is the side that is opposite the angle that is to be worked out.
- Adjacent: The ‘Adjacent’ is the side that is next to the angle.
Sine, Cosine and Tangent on the calculator
You will be performing calculations which involve sine, cosine and tangent. And the inverse of sine, cosine and tangent.
The inverse of sine is sin-1 sometimes also called asin or arcsin.
The inverse of cosine is cos-1 sometimes also called acos or arccos.
The inverse of tangent is tan-1 sometimes also called atan or arctan.
Using sine to find a missing angle
When we know any two sides of a right angled triangle we can use trigonometry to work out the angles. In the triangle shown below we know the ‘Opposite’ and ‘Hypotenuse’
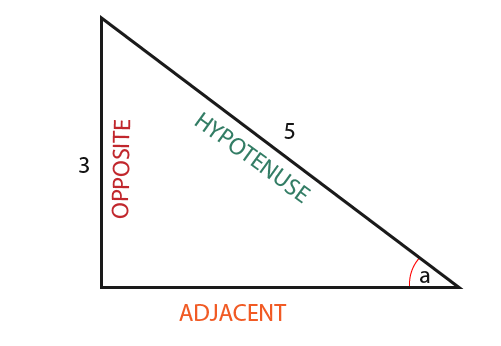
In this example we must find the angle between the hypotenuse and adjacent. There are 3 basic steps that you must follow to find the angle.
In this example we have been given the Opposite and Hypotenuse sides. The only function that we can use here is the sin function.
Substitute the known values into the equation to find the angle a°.
To find the angle of a° we must use the inverse of sine. The calculator should be helpful. Press the button and enter the value of 0.6. The calculator should provide the following result;
You may find the angles in radians or degrees. You have to make sure that you use the appropriate settings on your calculator.
Using the Cosine to find a missing angle
In this section we shall explore how to use cosine to find a missing angle. Whenever the Adjacent and Hypotenuse is given in a triangle we use cosine to find the missing angle.
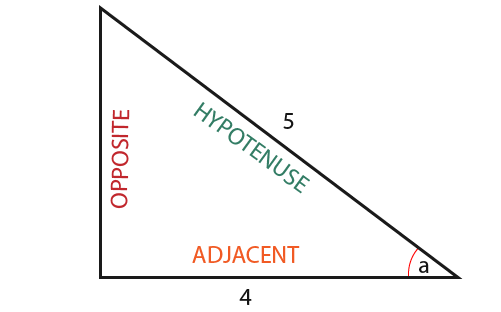
The sides of the triangle have been leballed below.

There 3 basic steps that you can follow to find the angle.
In this example. The hypotenuse and adjacent has been given. We must therefore use the cos(a) formula to find the angle.
Substitute the known values in the formula to find the unknown angle.
The angle a° is unknown and must be found. We must use the inverse of cos (a), the calculator should be useful here. Press and then (0.8) on the calculator, this should provide the result.
Using the tangent to find a missing angle
The methods that we have explored so far relied on us having knowledge of the length of the hypotenuse of the triangle. This is not always the case. The previous methods will not work without knowledge of the hypotenuse length, so we use tangent instead. In this example we know the ‘Opposite’ and ‘Adjacent’ in the triangle.
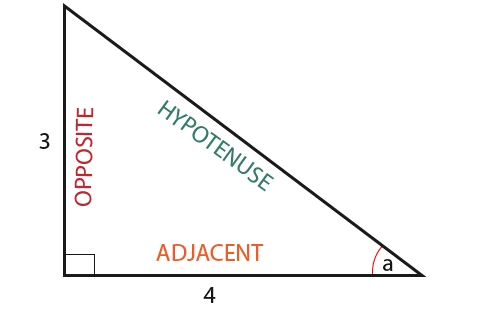
Again we follow 3 easy steps. In this example we have the adjacent and opposite side and we have to find the angle a. The sides of the triangle have been leballed below.

When given the opposite and adjacent sides the suitable formula is the tangent function.
Substitute in the known values to find the angle tan a°.
We’re trying to find the value of a° so we use the calculator by pressing followed by (0.75)
SOHCAHTOA Summary
We know now from the previous examples that …if the opposite and hypotenuse sides are given we use the sine formula;
…if the Adjacent and Hypotenuse sides are given then we use the cosine formula.
…if the Opposite and Adjacent sides are given then we use the tangent formula.
There is an easier way to remember these formulae.
Using abbreviations should help you remeber the formulae. Another way is to use sounds for example;
When you read the word you realise that it is a very sounding word which is easy to remember.
You may also use acronyms such as;
Another set of words that may help are;
You may also invent you own set of words but best use a combination of words based on historical facts that it is easier to remember.

Good