Y=mx+c
Here is a quick summary of this of this topic. This summary contains key points about the y=mx+c graphs. The graph below shows an example of a linear graph for equation y = mx + c
[graph id=”32″]
Here is another example of a graph with equation in the form y=mx+c;
[graph id=”30″]
m is the gradient (how steep the line is) and c is the intercept (where the line crosses the y-axis). The higher the m, the steeper the line…y = 5x is much steeper than y = 2x.
Plotting y=mx+c graphs
In this section we shall look at the basics of plotting linear (straight line) graphs which come in the form y=mx+c.
The graph of y=2x+1 has been shown below;
[graph id=”33″]
To plot a graph we usually draw a table and then find the value of y for the chosen x values. You need to make sure that the chosen xvalues are close to each other, for example 1 to 10. Below is the table that will help us plot the graph of y=2x+1.
| x | y |
|---|---|
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
Now we can plot these values on the graph as shown below.
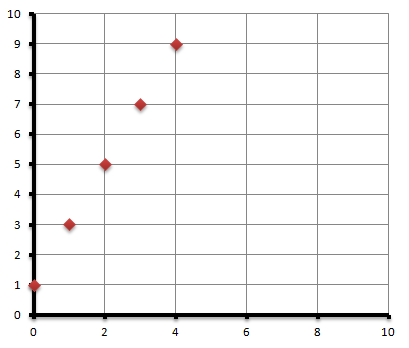
Now we join the plotted points with a single straight line.
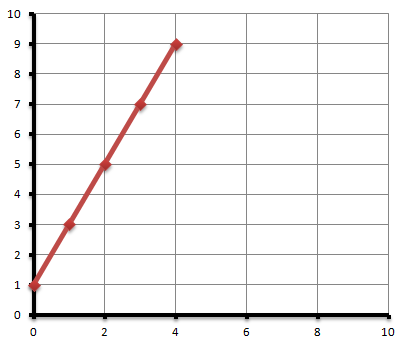
M and C in y=mx+c
In the equation y=mx+c m changes the steepness of the line. On the graph below we can see the variations in the lines whose gradient (m) is different. The lines still intercept at the same point on the y-axis.
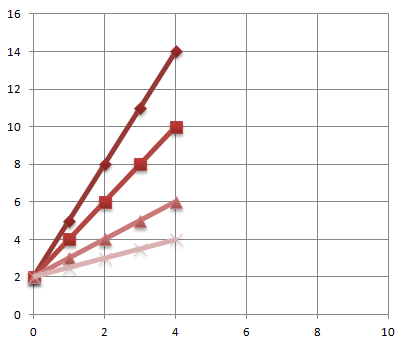
The C in y=mx+c changes where the line intercepts the y-axis.Changing the value of C moves the line down or upwards. This has been illustrated on the graph below. The lines on the graph have different values of y-axis intercept (c) but the same gradient.
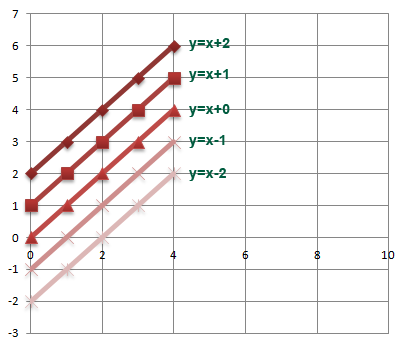
Gradient
Above we’ve seen that as the m value changes the steepness of the line changes. The steepness of the line in mathematics is known as gradient
We find the gradient on a straight line by dividing the number of units covered by a line across with the number of units covered by the line down. The following graph showis the line of y=½x+c
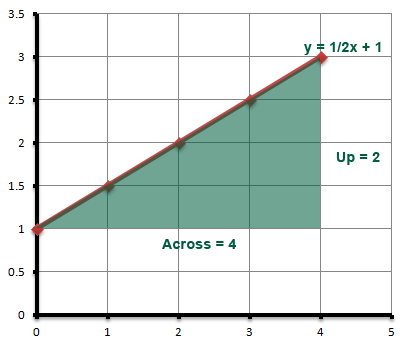
This should help us in counting the upwards and downwards units and keep the ratio the same no matter where we draw the triangle along the line.
Finding the equation of a straight line
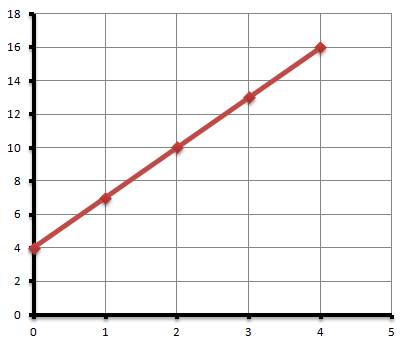
The equation of the graph above must be in the form of y=mx+c because the graph is a straight line. We need to find the values of m and c in the equation. We know that the c value indicates where the line intercepts the y-axis so;
![]()
We know that m is the gradient of the line and we find this by dividing the upwards coverage with the downwards coverage as shown on the graph below;
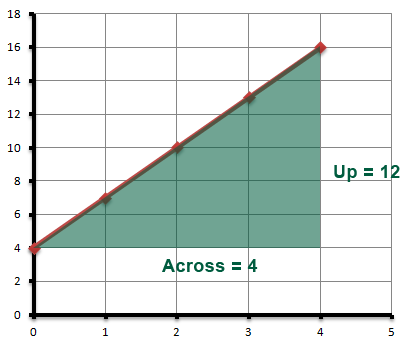
Therefore;
Now we know that the gradient is 3 and the line intercepts the y-axis at the coordinate (0, 4).The equation of the line becomes.

if the line .y=x+c touches the ellipse 2x^2+3y^2=1 then c=